Neural Network - with multiple inputs and neurons in hidden layer¶
In this note, I am going to train a neural network model with gradient decent estimation. This model will only have 2 direct inputs and 1 hidden layer with 3 neurons and logistic transform. The output layer will be activated with softmax.
Overview¶
This note will covere:
- Prepare the data
- Model and Cost function
- Backward propagation
- Momentum
- Code implementation
Parepare the data¶
The dataset is generated by the scikit-learn make_circles method. It will contain 2 labels, blue $(t=1)$ and red $(t=0)$, where the red class is a circular distribution that surrounds the distribution of the blue class.
# Python imports
import numpy as np # Matrix and vector computation package
import sklearn.datasets # To generate the dataset
import matplotlib.pyplot as plt # Plotting library
from matplotlib.colors import colorConverter, ListedColormap # Some plotting functions
from mpl_toolkits.mplot3d import Axes3D # 3D plots
from matplotlib import cm # Colormaps
# Allow matplotlib to plot inside this notebook
%matplotlib inline
# Set the seed of the numpy random number generator so that the tutorial is reproducable
np.random.seed(seed=1)
# Generate the dataset
X, t = sklearn.datasets.make_circles(n_samples=100, shuffle=False, factor=0.4, noise=0.1)
T = np.zeros((100,2)) # Define target matrix
T[t==1,1] = 1
T[t==0,0] = 1
# Separate the red and blue points for plotting
x_red = X[t==0]
x_blue = X[t==1]
print('shape of X: {}'.format(X.shape))
print('shape of T: {}'.format(T.shape))
As you can see the plot below, it's not linear separatable.
# Plot both classes on the x1, x2 plane
plt.plot(x_red[:,0], x_red[:,1], 'ro', label='class red')
plt.plot(x_blue[:,0], x_blue[:,1], 'bo', label='class blue')
plt.grid()
plt.legend(loc=1)
plt.xlabel('$x_1$', fontsize=15)
plt.ylabel('$x_2$', fontsize=15)
plt.axis([-1.5, 1.5, -1.5, 1.5])
plt.title('red vs blue classes in the input space')
plt.show()
Model and Cost Function¶
Model can be visualized as below:
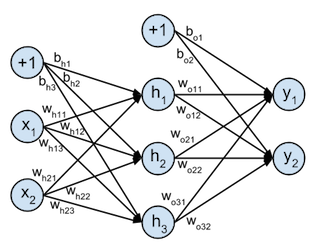
Input and Label¶
So for the input layer, we have 2 dimention inputs from N data points (Nx2): $$X = \begin{bmatrix} x_{11} & x_{12} \\ \vdots & \vdots \\ x_{N1} & x_{N2} \end{bmatrix}$$ And for output, we have 2 class (Nx2): $$T = \begin{bmatrix} t_{11} & t_{12}\\ \vdots & \vdots \\ t_{N1} & t_{N2} \end{bmatrix}$$
Where $t_{ij}=1$ if and only if the $i$-th input sample belongs to class $j$. So blue points are labelled T = [0 1] and red points are labelled T = [1 0].
Note in the model we added a bias term $b$ to $X$ that has value +1 for all rows.
Hidden Layer¶
The hidden layer has two set of parameters, $W_h$ (2x3) and bias term $b_h$ (1x3):
$$\begin{align} W_h = \begin{bmatrix} w_{h11} & w_{h12} & w_{h13} \\ w_{h21} & w_{h22} & w_{h23} \end{bmatrix} && \mathbf{b}_h = \begin{bmatrix} b_{h1} & b_{h2} & b_{h3} \end{bmatrix} \end{align}$$And we use logistic function for activation, hence $H$ (Nx3):
$$H = \sigma(z_h) =\sigma(X \cdot W_h + \mathbf{b}_h) = \frac{1}{1+e^{-(X \cdot W_h + \mathbf{b}_h)}} = \begin{bmatrix} h_{11} & h_{12} & h_{13} \\ \vdots & \vdots & \vdots \\ h_{N1} & h_{N2} & h_{N3} \end{bmatrix}$$Derivative of Logistic function¶
we will use the derivative of Logistic function in backward propagation. So writing down here in advance.
(1) $$\frac{\partial h_i}{\partial z_{hi}} = \frac{\partial \sigma(z_{hi})}{\partial z_{hi}} = \frac{\partial \frac{1}{1+e^{-z_{hi}}}}{\partial z_{hi}} = \frac{-1}{(1+e^{-z_{hi}})^2} *e^{-z_{hi}}*-1 = \frac{1}{1+e^{-z_{hi}}} \frac{e^{-z_{hi}}}{1+e^{-z_{hi}}} = \sigma(z_{hi}) * (1- \sigma(z_{hi})) = h_i (1-h_i)$$
Output layer¶
The output layer has two set of parameters, $W_o $ (3x2) and bias term $b_o$ (2x1):
$$\begin{align} W_o = \begin{bmatrix} w_{o11} & w_{o12} \\ w_{o21} & w_{o22} \\ w_{o31} & w_{o32} \end{bmatrix} && \mathbf{b}_o = \begin{bmatrix} b_{o1} & b_{o2} \end{bmatrix} \end{align}$$And we use softmax function for activation, hence $Y$ (Nx2):
with $\varsigma$ the softmax function. In our example data, $C=2$ as we have 2 class red and blue.
Derivative of Softmax function¶
we will use the derivative of Softmax function in backward propagation. So writing down here in advance.
For $\Sigma_C = \sum_{d=1}^C e^{z_d} \, \text{for} \; c = 1 \cdots C$ so that $y_c = e^{z_c} / \Sigma_C$, ${\partial y_i}/{\partial z_j}$ of the output $y$ of the softmax function with respect to its input $z$ can be calculated as:
(2) $$ \begin{split} \text{if} \; i = j :& \frac{\partial y_i}{\partial z_i} = \frac{\partial \frac{e^{z_i}}{\Sigma_C}}{\partial z_i} = \frac{e^{z_i}\Sigma_C - e^{z_i}e^{z_i}}{\Sigma_C^2} = \frac{e^{z_i}}{\Sigma_C}\frac{\Sigma_C - e^{z_i}}{\Sigma_C} = \frac{e^{z_i}}{\Sigma_C}(1-\frac{e^{z_i}}{\Sigma_C}) = y_i (1 - y_i)\\ \text{if} \; i \neq j :& \frac{\partial y_i}{\partial z_j} = \frac{\partial \frac{e^{z_i}}{\Sigma_C}}{\partial z_j} = \frac{0 - e^{z_i}e^{z_j}}{\Sigma_C^2} = -\frac{e^{z_i}}{\Sigma_C} \frac{e^{z_j}}{\Sigma_C} = -y_i y_j \end{split} $$
Code for forward step¶
We can at first code the functions for forward step.
# Define the logistic function. - for hidden layer activation.
def logistic(z):
return 1 / (1 + np.exp(-z))
# Define the softmax function
def softmax(z):
return np.exp(z) / np.sum(np.exp(z), axis=1, keepdims=True)
# Function to compute the hidden activations
def hidden_activations(X, Wh, bh):
return logistic(X.dot(Wh) + bh)
# Define output layer feedforward
def output_activations(H, Wo, bo):
return softmax(H.dot(Wo) + bo)
# Define the neural network function
def nn(X, Wh, bh, Wo, bo):
return output_activations(hidden_activations(X, Wh, bh), Wo, bo)
# Define the neural network prediction function that only returns
# 1 or 0 depending on the predicted class
def nn_predict(X, Wh, bh, Wo, bo):
return np.around(nn(X, Wh, bh, Wo, bo))
Cost Function¶
The parameter set $w$ can be optimized by maximizing the likelihood:
The likelihood can be described as join distribution of $t\;and\;z\;$given $\theta$:
$$P(\mathbf{t},\mathbf{z}|\theta) = P(\mathbf{t}|\mathbf{z},\theta)P(\mathbf{z}|\theta)$$We don't care the probability of $\mathbf{z}$ so
$$\mathcal{L}(\theta|\mathbf{t},\mathbf{z}) = P(\mathbf{t}|\mathbf{z},\theta)$$It can be written as $P(\mathbf{t}|\mathbf{z})$ for fixed $\theta$. Since each $t_i$ is dependent on the full $\mathbf{z}$, and only 1 class can be activated in the tt we can write:
$$P(\mathbf{t}|\mathbf{z}) = \prod_{i=c}^{C} P(t_c|\mathbf{z})^{t_c} = \prod_{i=c}^{C} \varsigma(\mathbf{z})_c^{t_c} = \prod_{i=c}^{C} y_c^{t_c}$$Instead of maximizing this likelihood, it can also be done by minimizing the negative log-likelihood:
The cross-entropy error function $\xi$ for multiple class of sample size $n$ can be defined as:
$$\xi(T,Y) = \sum_{i=1}^n \xi(\mathbf{t}_i,\mathbf{y}_i) = - \sum_{i=1}^n \sum_{i=c}^{C} t_{ic} \cdot log( y_{ic})$$Note $Y$ will be activated by softmax in output layer as we defined above.
Derivative of the cross-entropy cost function for the softmax function¶
The derivative ${\partial \xi}/{\partial z_i}$ of the cost function with respect to the softmax input $z_i$ can be calculated as (Note below use (2) the derivative of softmax function):
(3) $$ \begin{split} \frac{\partial \xi}{\partial z_i} & = - \sum_{j=1}^C \frac{\partial t_j log(y_j)}{\partial z_i}{} = - \sum_{j=1}^C t_j \frac{\partial log(y_j)}{\partial z_i} = - \sum_{j=1}^C t_j \frac{1}{y_j} \frac{\partial y_j}{\partial z_i} \\ & = - \frac{t_i}{y_i} \frac{\partial y_i}{\partial z_i} - \sum_{j \neq i}^C \frac{t_j}{y_j} \frac{\partial y_j}{\partial z_i} = - \frac{t_i}{y_i} y_i (1-y_i) - \sum_{j \neq i}^C \frac{t_j}{y_j} (-y_j y_i) \\ & = - t_i + t_i y_i + \sum_{j \neq i}^C t_j y_i = - t_i + \sum_{j = 1}^C t_j y_i = -t_i + y_i \sum_{j = 1}^C t_j \\ & = y_i - t_i \end{split} $$
Backward propagation¶
During the backward step, what's important is to get the error gradient in each layer.
Gradient of output layer¶
The error gradient $\delta_{o}$ of this cost function at the softmax output layer is simply (from (3)):
$$\delta_{o} = \frac{\partial \xi}{\partial Z_o} = Y - T$$As $Z_o = H \cdot W_o + \mathbf{b}_o$, so the output grandient over all $N$ samples is computed :
$$\frac{\partial \xi}{\partial \mathbf{w}_{oj}} = \frac{\partial Z_{o}}{\partial \mathbf{w}_{oj}} \frac{\partial Y}{\partial Z_{o}} \frac{\partial \xi}{\partial Y} = \frac{\partial Z_{o}}{\partial w_{oji}} \frac{\partial \xi}{\partial Z_o} = \sum_{i=1}^N h_{ij} (\mathbf{y}_i - \mathbf{t}_i) = \sum_{i=1}^N h_{ij} \delta_{oi}$$In matrix form:
$$\frac{\partial \xi}{\partial W_o} = H^T \cdot (Y-T) = H^T \cdot \delta_{o}$$For bias term $b_o$:
$$\frac{\partial \xi}{\partial \mathbf{b}_{o}} = \frac{\partial Z_{o}}{\partial \mathbf{b}_{o}} \frac{\partial Y}{\partial Z_{o}} \frac{\partial \xi}{\partial Y} = \sum_{i=1}^N 1 * (\mathbf{y}_i - \mathbf{t}_i) = \sum_{i=1}^N \delta_{oi}$$Gradient of hidden layer¶
The error gradient $\delta_{h}$ of this cost function at the hidden layer can be defined as:
$$\delta_{h} = \frac{\partial \xi}{\partial Z_h} = \frac{\partial H}{\partial Z_h} \frac{\partial \xi}{\partial H} = \frac{\partial H}{\partial Z_h} \frac{\partial Z_o}{\partial H} \frac{\partial \xi}{\partial Z_o}$$As $Z_h = X \cdot W_h + \mathbf{b}_h$, $\delta_{h}$ will also result in a $N×3$ matrix. We use (1) and (2) to get result below.
Note the gradients that backpropagate from the previous layer via the weighted connections are summed for each $h_{ij}$
In matrix form with notation $\circ$ for elementwise product:
The hidden layer gradient then can be defined as:
$$\frac{\partial \xi}{\partial \mathbf{w}_{hj}} = \frac{\partial Z_{h}}{\partial \mathbf{w}_{hj}} \frac{\partial H}{\partial Z_{h}} \frac{\partial \xi}{\partial H} = \frac{\partial Z_{h}}{\partial \mathbf{w}_{hj}} \frac{\partial \xi}{\partial Z_h} = \sum_{i=1}^N x_{ij} \delta_{hi}$$For bias term $b_h$:
$$\frac{\partial \xi}{\partial \mathbf{b}_{h}} = \frac{\partial Z_{h}}{\partial \mathbf{b}_{h}} \frac{\partial H}{\partial Z_{h}} \frac{\partial \xi}{\partial H} = \sum_{j=1}^N \delta_{hj}$$Code for cost and backward gradient¶
# Define the cost function
def cost(Y, T):
return - np.multiply(T, np.log(Y)).sum()
# Define the error function at the output
def error_output(Y, T):
return Y - T
# Define the gradient function for the weight parameters at the output layer
def gradient_weight_out(H, Eo):
return H.T.dot(Eo)
# Define the gradient function for the bias parameters at the output layer
def gradient_bias_out(Eo):
return np.sum(Eo, axis=0, keepdims=True)
# Define the error function at the hidden layer
def error_hidden(H, Wo, Eo):
# H * (1-H) * (E . Wo^T)
return np.multiply(np.multiply(H,(1 - H)), Eo.dot(Wo.T))
# Define the gradient function for the weight parameters at the hidden layer
def gradient_weight_hidden(X, Eh):
return X.T.dot(Eh)
# Define the gradient function for the bias parameters at the output layer
def gradient_bias_hidden(Eh):
return np.sum(Eh, axis=0, keepdims=True)
Momentum¶
Model like this is highly unlikely to have convex cost functions and we might easily get a local minimum with gradient decent. Momentum is created to solve this. It's probably the most popular extension of the backprop algorithm.
Momentum can be defined:
$$\begin{split} V(i+1) & = \lambda V(i) - \mu \frac{\partial \xi}{\partial \theta(i)} \\ \theta(i+1) & = \theta(i) + V(i+1) \end{split} $$Where $V(i)$ is the velocity of the parameters at iteration $i$ and 0< $\lambda$ <1 shows how much the velocity decreases due to 'resistance' and $\mu$ the learning rate.
Note here we are using previous $V(i)$ to update $V(i+1)$. The initial $V(0)$ should be nearly 0 so $V(1)$ is $\lambda$ (say, 0.9)*0 $-\mu \frac{\partial \xi}{\partial \theta(0)}$ (say, -1) = -1 and in iteration=2 the $V(i)$ is the same direction (say, -0.5) then $V(2)$ will become bigger (-0.9 - 0.5 = -1.4) and smaller if opposite direction (say. 0.5 -> -0.9 + 0.5 = -0.4).
Essentially, it's just like we push a ball down a hill. The ball accumulates momentum as it rolls downhill, becoming faster and faster on the way. The same thing happens to our parameter updates: The momentum term increases for dimensions whose gradients point in the same directions and reduces updates for dimensions whose gradients change directions. As a result, we gain faster convergence and reduced oscillation.
We can code backprop with momentum as below.
# Define the update function to update the network parameters over 1 iteration
def backprop_gradients(X, T, Wh, bh, Wo, bo):
# Compute the output of the network
# Compute the activations of the layers
H = hidden_activations(X, Wh, bh)
Y = output_activations(H, Wo, bo)
# Compute the gradients of the output layer
Eo = error_output(Y, T)
JWo = gradient_weight_out(H, Eo)
Jbo = gradient_bias_out(Eo)
# Compute the gradients of the hidden layer
Eh = error_hidden(H, Wo, Eo)
JWh = gradient_weight_hidden(X, Eh)
Jbh = gradient_bias_hidden(Eh)
return [JWh, Jbh, JWo, Jbo]
def update_velocity(X, T, ls_of_params, Vs, momentum_term, learning_rate):
# ls_of_params = [Wh, bh, Wo, bo]
# Js = [JWh, Jbh, JWo, Jbo]
Js = backprop_gradients(X, T, *ls_of_params)
return [momentum_term * V - learning_rate * J for V,J in zip(Vs, Js)]
def update_params(ls_of_params, Vs):
# ls_of_params = [Wh, bh, Wo, bo]
# Vs = [VWh, Vbh, VWo, Vbo]
return [P + V for P,V in zip(ls_of_params, Vs)]
Code Implementaion¶
# Run backpropagation
# Initialize weights and biases
init_var = 0.1
# Initialize hidden layer parameters
bh = np.random.randn(1, 3) * init_var
Wh = np.random.randn(2, 3) * init_var
# Initialize output layer parameters
bo = np.random.randn(1, 2) * init_var
Wo = np.random.randn(3, 2) * init_var
# Parameters are already initilized randomly with the gradient checking
# Set the learning rate
learning_rate = 0.02
momentum_term = 0.9
# define the velocities Vs = [VWh, Vbh, VWo, Vbo]
Vs = [np.zeros_like(M) for M in [Wh, bh, Wo, bo]]
# Start the gradient descent updates and plot the iterations
nb_of_iterations = 300 # number of gradient descent updates
lr_update = learning_rate / nb_of_iterations # learning rate update rule
ls_costs = [cost(nn(X, Wh, bh, Wo, bo), T)] # list of cost over the iterations
for i in range(nb_of_iterations):
# Update the velocities and the parameters
Vs = update_velocity(X, T, [Wh, bh, Wo, bo], Vs, momentum_term, learning_rate)
Wh, bh, Wo, bo = update_params([Wh, bh, Wo, bo], Vs)
ls_costs.append(cost(nn(X, Wh, bh, Wo, bo), T))
# Plot the cost over the iterations
plt.plot(ls_costs, 'b-')
plt.xlabel('iteration')
plt.ylabel('$\\xi$', fontsize=15)
plt.title('Decrease of cost over backprop iteration')
plt.grid()
plt.show()
Visualization of the trained classifier¶
The classifier we just trianed is circled around and between the blue and red class. It's non-linear and hence be able to correctly classify red and blue.
# Plot the resulting decision boundary
# Generate a grid over the input space to plot the color of the
# classification at that grid point
nb_of_xs = 200
xs1 = np.linspace(-2, 2, num=nb_of_xs)
xs2 = np.linspace(-2, 2, num=nb_of_xs)
xx, yy = np.meshgrid(xs1, xs2) # create the grid
# Initialize and fill the classification plane
classification_plane = np.zeros((nb_of_xs, nb_of_xs))
for i in range(nb_of_xs):
for j in range(nb_of_xs):
pred = nn_predict(np.asmatrix([xx[i,j], yy[i,j]]), Wh, bh, Wo, bo)
classification_plane[i,j] = pred[0,0]
# Create a color map to show the classification colors of each grid point
cmap = ListedColormap([
colorConverter.to_rgba('w', alpha=0.30),
colorConverter.to_rgba('g', alpha=0.30)])
# Plot the classification plane with decision boundary and input samples
plt.contourf(xx, yy, classification_plane, cmap=cmap)
# Plot both classes on the x1, x2 plane
plt.plot(x_red[:,0], x_red[:,1], 'ro', label='class red')
plt.plot(x_blue[:,0], x_blue[:,1], 'bo', label='class blue')
plt.grid()
plt.legend(loc=1)
plt.xlabel('$x_1$', fontsize=15)
plt.ylabel('$x_2$', fontsize=15)
plt.axis([-1.5, 1.5, -1.5, 1.5])
plt.title('red vs blue classification boundary')
plt.show()
Transformation of the input domain¶
You can see from the plot below. the 2-dimentions input have been project into 3-dimension space (hidden layer) and become liner separable.
# Plot the projection of the input onto the hidden layer
# Define the projections of the blue and red classes
H_blue = hidden_activations(x_blue, Wh, bh)
H_red = hidden_activations(x_red, Wh, bh)
# Plot the error surface
fig = plt.figure()
ax = Axes3D(fig)
ax.plot(np.ravel(H_blue[:,2]), np.ravel(H_blue[:,1]), np.ravel(H_blue[:,0]), 'bo')
ax.plot(np.ravel(H_red[:,2]), np.ravel(H_red[:,1]), np.ravel(H_red[:,0]), 'ro')
ax.set_xlabel('$h_1$', fontsize=15)
ax.set_ylabel('$h_2$', fontsize=15)
ax.set_zlabel('$h_3$', fontsize=15)
ax.view_init(elev=10, azim=-40)
plt.title('Projection of the input X onto the hidden layer H')
plt.grid()
plt.show()
The sample codes in this note come from peterroelants.github.io where providing more details on neural netwrok and deep learning. It's very informative and highly recommanded. Here is more like my personal memo.